I recently tried watching a movie on YouTube with the automatic subtitles feature turned on. The result was hilarious. “Good bye!” was routinely transcribed as “Good behind!” And the exercise confirmed my belief/prejudice that there is no such thing as ‘artificial intelligence’. All intelligence is natural and all living creatures possess it in equal and abundant measure. All computers by contrast are obstinately dumb.

The frustration of watching a film with computer-generated subtitles also provides some solace for language learners who struggle with listening skills. Complex algorithms developed by the boffins at Google suck at this much worse than you do!

I subsequently went online and did a little research into how the coddled techies at Google come up with these ‘speech recognition’ algorithms and I discovered that they use something called Markov chains. So I had to Google that too, fully aware that, by the very act of doing so, I might be entering into a perilous feedback-loop sample bias.

Not being a techie person myself, I spent my first evening of research reading up about Prof. Markov himself and wondering at 1) how Markov originally discovered this mathematical truth by examining patterns of alliteration in classic Russian literature; 2) how this late 19th century entitled nerd and his protégés somehow all managed to escape Stalin’s purges; and 3) how this arcane marvel of Soviet mathematical discovery somehow made its way across the Atlantic (or the Arctic) to become a mainstay of modern-day Western informatics.

Day 2 of my research into Markov chains, I started watching a series of lectures on them that were easy enough for me to understand. On YouTube of course—but with the subtitles firmly in the off setting.

Three days later, I feel I have a fairly good grasp of the basics of what Markov chains are, although I am still puzzled and highly skeptical as to how they relate to speech recognition algorithms.

Markov chains concern chains of probability over time. In classical probability theory, each event is independent of the other, so that, however many times you toss a coin, the probability of it coming up heads or tails (providing the coin is not doctored) is more or less 50% either way.

In Markov chains, however, each iteration of an event changes the probability of the next in a predictable way. So, rather than each toss of the coin being independent of the others, throwing heads once, for example, increases the likelihood of throwing heads again on the next throw. Let’s say, for the sake of argument, that throwing heads on one throw makes throwing heads on the next throw 10 percentage points more likely. So the probability of throwing heads the next time is 60%, while the probability of either result after throwing tails remains the same. So, the probability of throwing heads followed by heads is 0.6, that of heads followed by tails 0.4, while the odds of throwing heads or tails after throwing tails remains 0.5 either way. [Ideally, I would insert a matrix here, but I haven’t been able to work out how to do matrices on WordPress, so you’ll just have to imagine that, if you can.]

Supposing that the first toss was 50:50 (actually it doesn’t matter what the initial odds are), the odds on the second toss will be 0.3 for heads to heads, 0.2 for heads to tails, 0.25 for tails to heads and 0.25 for tails to tails. [Again, this looks nicer or at least neater in matrix form.]

Adding up the probabilities for heads and tails on the second throw, we get 0.55 for heads and 0.45 for tails. The probability of throwing heads, unsurprisingly, has gone up.

But what will happen, if we repeat this process over and over again? Intuition seems to tell us that heads will become increasingly more likely. But intuition is a bad guide in mathematics, just as mathematics is a bad guide in real life.
In fact, if we repeat the process just 20 times, the probability of either outcome stabilizes and thereafter remains the same ad infinitum. You will get heads 5 times out of 9 and tails 4 times out of nine. That is the magic of Markov chains…

We can go further and other patterns emerge. If we increase the likelihood of a throw of heads generating a subsequent identical throw steadily from 0 to 1 by increments of 0.1, while holding the probability of tails to tails steady at fifty-fifty, we get the following sequence of steady end-state probabilities for each scenario, as we approach an infinite number of chained subsequent throws: {5/15, 5/14, 5/13 ,5/12 ,5/11 ,5/10 ,5/9 ,5/8 ,5/7 ,5/6 ,5/5}. The pattern is clear.

We can even project the Markov chain for this series backwards and forwards into ‘imaginary’ realms of probability, in which odds can be negative (i.e. less than zero) or more than 100%, and we get the following graph, which looks like some kind of logo or religious symbol.

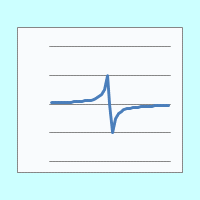
I never cease to be enchanted by the beauty of mathematics, but it is a cold and cruel beauty and, if we are not wary, it is wont to entrap us forever, Circe-like, on its fantasy island and turn us into dumb beasts.

Markov chains have taken us off on a flight of fancy. Most of the positions on this beautifully symmetrical graph do not and cannot exist. It is very doubtful, to say the least, whether the simple Markov assumption that one state directly determines the state of the next, without taking into account previous states, is at all valid for anything approaching real life.

Besides, numbers do not even exist in real life. They are just a figment of our imagination.

But, “Hey!” I hear you collectively saying. Didn’t mathematics enable us to build pyramids and develop the internal combustion engine and send men (but not women) to the moon? Yes it did. But these things—pyramidal monuments, motor cars and space rockets—are in themselves embodiments of abstractions and, if we look into the social history that engendered them, we will find that they depended for their invention on some very human, very emotional, (usually very masculine) and ultimately very perverse will or whim.

Note to self and others: Markov chains, for all their cold enchanting beauty, will never replace the messy, flawed, ambiguous process of two or more people sitting down and listening to one another. Turn off your Markov-chain-based prostheses; listen imperfectly to the imperfect churning chaos of the real human world, not the Siren song.